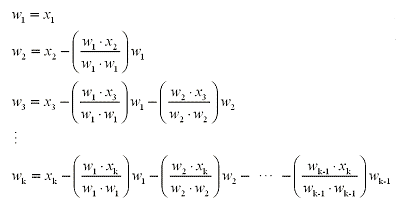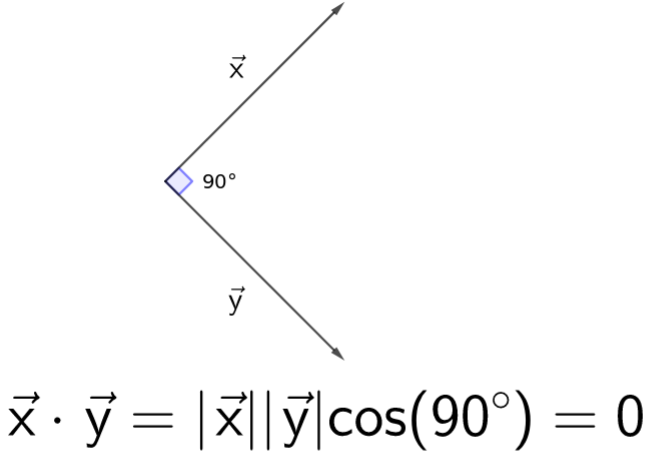Smart Tips About How To Check For Orthogonality

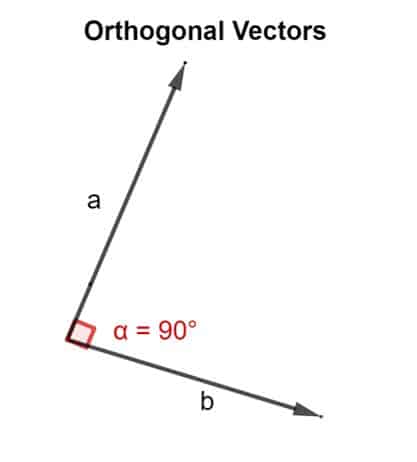
They make an angle of 90° (π/2 radians), or one of the vectors.

How to check for orthogonality. So, the dot product of the vectors a and b would be something as shown. The sum of each set of coefficients is still equal to zero, but the sum of their cross products is not equal to zero, namely [ (1 × 0) + (−1 × +1) + (0 × −1)] = −1. To check if a given matrix is orthogonal, first find the transpose of that matrix.

The idea is simple, we first find transpose of matrix. Returns a value 1 if the rows are pairwise orthogonal, else return 0. Since we get the identity matrix, then we.

Orthonormal means that, in addition to. Ay } and b = { bx; What is the condition of orthogonality?

Treat = a + b1*x1 +. Errors can be viewed on command line with regular output, or you can pipe errors to a file using: 4.2/5 ( 32 votes) to determine if a matrix is orthogonal, we need to multiply the matrix by it's transpose, and see if we get the identity matrix.

X 1 ⋅ x 2 + y 1 ⋅ y 2 + z 1 ⋅ z 2 = 0, x 1 ⋅ x 3 + y 1 ⋅ y 3 + z 1 ⋅ z 3 = 0, x 2 ⋅ x 3 + y 2 ⋅ y 3 + z 2 ⋅ z 3 = 0. To do this, take your set of x variables (x1, x2,., x20) and run the following: Then, multiply the given matrix with the transpose.

1 1 − 1 2 + 0 3 0 1 + 1 2 − 1 3. In euclidean space, two vectors are orthogonal if and only if their dot product is zero, i.e. To verify orthogonality, check the following: